Oddělení neporušuje druhý zákon termodynamiky, protože oddělené fáze oleje a vody jsou nízkoenergetické.

Molekuly vody vzájemně silně interagují a tvoří vodíkové vazby. Protony vody jsou sdíleny mezi dvěma atomy kyslíku dvou různých molekul vody a vytvářejí neustále se měnící síť molekul. Molekuly vody nemají silné intermolekulární interakce s molekulami oleje.

Čím více jsou obě fráze smíchány, tím více molekul vody je na povrchu rozhraní. Molekuly vody na povrchu rozhraní se nemohou plně účastnit intermolekulárních interakcí s jinými molekulami vody, takže se jedná o stav s vyšší energií.

Aby mohl proces spontánně proběhnout, musí se Gibbsova volná energie (G) snížit.

$ \ Delta G = \ Delta HT \ Delta S $

Entropie (S) je tedy pouze částí úvah. Je třeba vzít v úvahu také entalpii (H) a teplotu (T). V tomto případě pokles entalpie (H) v důsledku energie intermolekulárních interakcí vyrovnává pokles entropie (S). Tento proces je exotermický proces.

I když chybí gravitace, je stále termodynamicky příznivé, aby se fáze oddělily, aby se minimalizovala povrchová plocha mezi povrchy, stejně jako sférický pokles vody, který je nejnižší gravitační stav.

Předpovídal bych, že při absenci gravitace by nejnižší energetický stav zálivky byl sféra vodní fáze obklopená sférickým obalem olejové fáze.

Odpověď DavePhD vysvětluje specifika. Separace snižuje entalpii směsi oleje a vody. Ale je tu ještě jeden krok:

Když entalphy obvazu poklesne o $ \ Delta H $, způsobí to entropie obvazu a jeho okolního prostředí na zvýšení o $ \ Delta H / T $.

Důvod je: Snížení entalpie uvolňuje teplo, což (mírně) zvyšuje teplotu obvazu a jeho nádoby a vnitřní místnosti. Vyšší teplota znamená více entropie.

Takže ve větším obrazu to ve skutečnosti zvyšuje entropii.

Zde je pokus spojit dvě další odpovědi:

Systém je zálivka, která je ve styku se vzduchem a vytváří tepelný zásobník při konstantní teplotě $ T $ (izotermická). Vše je také pod stálým tlakem $ P $ (isobarické). Porovnáváme počáteční, smíšený s konečnými, oddělenými stavy systému.

DavePhD uvádí, že k demixování dochází, protože výsledek má nižší energii, což zní definitivně. Ztráta energie obvazu je však ziskem nádrže (zachováním energie), takže celková energie se nezmění a člověk by se mohl začít cítit trochu nejistě.

Poté (správně) uvádí, že změna Gibbsovy volné energie: $$ \ Delta G_ {sys} = \ Delta H_ {sys} - T \ Delta S_ {sys} $$ musí být negativní, aby reakce proběhla spontánně, a upozorňuje, že „entropie (S) je pouze část protiplnění “. Přidal jsem indexy, které naznačují, že tato množství jsou Gibbsova volná energie, entalpie a entropie systému.

V tomto okamžiku může být někdo vyškolený k přesvědčení, že entropie musí vždy narůstat, poněkud zmatený.

SteveB, který si uvědomuje tento potenciální zmatek, spojuje tento výsledek s celkovou entropií systém plus zásobník. Pro izotermický, izobarický proces, bez ohledu na to, zda systém provádí práci, $ \ Delta H_ {sys} $ je množství tepla přidaného do systému ze zásobníku. Změna entropie nádrže (nikoli systému + nádrže) je tedy následující: $$ \ Delta S_ {res} = - \ frac {\ Delta H_ {sys}} {T} $ $

Změna celkové entropie $ S_ {tot} $ je pak: $$ \ Delta S_ {tot} = \ Delta S_ {sys} + \ Delta S_ {res} = \ Delta S_ {sys } - \ frac {\ Delta H_ {sys}} {T} = - \ frac {\ Delta G_ {sys}} {T} $$

Takže pro izotermickou, izobarickou reakci, pokles v Gibbsově volné energii systému odpovídá zvýšení celkové entropie (systém + nádrž). Jak se očekávalo (doufalo?), Spontánní reakce skutečně zvyšují (celkovou) entropii!

Pamatujte, že odmíchání není nutně spontánní: proces rozmíchání musí generovat dostatek tepla, aby se entropie nádrže zvýšila o více než pokles entropie systému.

Nakonec, pokud je proces izobarický, ale ne izotermický, část emitovaného tepla zvyšuje teplotu (a tedy entropii) systému (jak uvádí SteveB), takže výpočet již není tak jednoduché. Ve skutečnosti $ \ Delta G_ {sys} = 0 $ již není prahovou hodnotou pro spontánní reakce v tomto stavu, protože pro nekonečně malý reverzibilní proces:

$$ dG = -S \, dT + V \, dP $$

takže $ dG \ ne 0 $, pokud $ dT \ ne 0 $. Místo toho je nutné vypočítat změnu celkové entropie, aby se určila spontánnost.

Krátká odpověď:

Krátká odpověď je, že přechod od míchaného salátového dresingu ke dvěma vrstvám je exotermický a toto uvolňování tepla vytváří nárůst entropie. Pro všechny účely a účely je tento proces analogický s exotermickou chemickou reakcí, jako je spalování.

Podobně se nádoba naplněná kuličkovými ložisky může spontánně usadit do šestihranného těsného obalu dohoda. Stejně jako pouzdro na zálivku to dává vizuální vzhled většího řádu, ale ve skutečnosti to není porušení zákona $ \ Delta S_ \ text {univ} \ geq 0 $ , protože energie se uvolňuje při usazování, které se přeměňuje na neuspořádané teplo.

Mírně delší odpověď:

Jsem hrozný v termodynamice, takže může být zapotřebí několik oprav aby to bylo přísné, ale můžete se pokusit vysvětlit věci takto: nechte salátový dresink být pod vlivem gravitace obsažen v pevné, tepelně vodivé nádobě Celková energie systému může být zapsána jako $$ U = m_ \ text {w} \ overline {U} _ \ text {w, bulk} + m_ \ text {o} \ overline {U} _ \ text {o, bulk} + \ int_V \ rho (\ mathbf {r}) V (\ mathbf {r}) \, d \ mathbf {r} + \ int_ {S_d} \ gamma_ \ text {w, o} \, dS + \ int_ {S_c} \ gamma (S) \, dS $$ kde $ \ overline {U} _ \ text {w, bulk} $ je celková objemová vnitřní energie na hmotnost vody (a podobná pro $ U_ \ text {o, bulk}) $ , $ m_ \ text {w} $ a $ m_ \ text {o} $ jsou celkové hmotnosti vody a oleje, $ \ rho (\ mathbf {r}) $ je hustota kapaliny v místě $ \ mathbf {r} $ v nádobě, $ V (\ mathbf {r}) $ je gravitační potenciál, $ S_d $ je sada rozhraní olej-voda, $ \ gamma_ \ text {w, o} $ je povrchové napětí oleje a vody, $ S_c $ je hranice stěn kontejneru a $ \ gamma (S) $ je povrchové napětí stěny kapaliny typu kapaliny na hraničním místě $ S $ .

První a druhý výraz v podstatě popisují objemovou (objemovou) energii vody a oleje, třetí uvažuje gravitační energii systému, čtvrtý uvažuje energii způsobenou rozhraními olej-voda a pátý považuje energii způsobenou rozhraním nádoby na kapalinu.

Linearizace gravitace jako $ V (\ mathbf {r}) \ cca g | \ mathbf {r } | $ , $ U $ lze přepsat jako $$ U = m_ \ text {w} \ overline {U} _ \ text {w, bulk} + m_ \ text {o} \ overline {U} _ \ text {o, bulk} + \ rho_ \ text {w} m_ \ text {w} \ langle h_ \ text {w} \ rangle + \ rho_ \ text {o} m_ \ text {o} \ langle h_ \ text {o} \ rangle \\ + \ gamma_ \ text {w, o} A_d + \ gamma_ \ text {w, c } A _ {\ text {w, c}} + \ gamma_ \ text {o, c} A _ {\ text {o, c}} $$ kde $ \ langle h_ \ text {w} \ rangle $ a $ \ langle h_ \ text {o} \ rangle $ jsou očekávané hodnoty výšky vody a oleje uvnitř kontejneru, $ A_d $ je celková plocha rozhraní kapiček oleje a vody a $ A _ {\ text {o, c}} $ a $ A _ {\ text {w, c}} $ jsou celková plocha kontaktu oleje a vody se stěnami kontejneru a $ \ gamma_ \ text {w, c} $ a $ \ gamma_ \ text {o, c} $ jsou povrchová napětí nádoby na vodu a oleje.

Změna konfigurace vytvoří změnu vnitřní energie $$ \ Delta U = \ rho_ \ text {w} m_ \ text {w} \ langle \ Delta h_ \ text {w} \ rangle + \ rho_ \ text {o} m_ \ text {o} \ langle \ Delta h_ \ text {o} \ rangle + \ gamma_ \ text {w, o} \ Delta A_d + \ gamma_ \ text {w, c} \ Delta A _ {\ text {w, c}} + \ gamma_ \ text { o, c} \ Delta A _ {\ text {o, c} }. $$ Všimněte si, že $ \ Delta U<0 $ pro přechod od míchaného salátového dresingu do dvou oddělených vrstev.

Přebytek energie je přeměněna na teplo, tj. $ \ Delta U = \ Delta q $ , které je poté ztraceno okolím přes stěny kontejneru. Změna entropie je pak $$ \ Delta S = \ Delta S_ \ text {sys} + \ Delta S_ \ text {surr} = - \ frac {\ Delta U} {T_ \ text {sys}} + \ frac {\ Delta U} {T_ \ text {surr}} >0 $$ od $ T_ \ text {sys} >T_ \ text { surr} $ za to, že dojde k přenosu tepla.

(Omlouvám se, pokud jsem v předchozím odstavci zmařil základní termodynamické vztahy).

Můj pohled je jednodušší, na řádcích, které již citujete, že směs v kontejneru není izolovaným systémem.

Stejně jako u krystalů vycházejících z řešení je třeba vzít v úvahu celý systém, když cituji druhý zákon. V tomto případě dojde k výměně tepla s prostředím i zářením, protože molekuly spadají do stavu nižší energie, který charakterizuje separaci, a proto nejsou uzavřeny.

Odpověď bez matematiky:

Kontintuitivní částí je mylný předpoklad, že stav oddělování „čistého“ octa a „čistého“ oleje představuje vyšší energii nebo více „uspořádaného stavu“ než smíchaný ocet a olej.

To je zpět. „Čisté“ stavy jsou nejnižší energetické stavy a smíšené nejvyšší.

Když systém vzájemně rozšleháte, přidáte energii do systému ocet / voda a olej. Mechanický dopad šlehače ve skutečnosti napěňuje vodní a olejové složky dohromady na vysoce složité struktury.

Analogicky je oddělený stav jako mít na zemi hromadu skal. Metla zvedá kameny a hromadí je do struktur. Jelikož entropie způsobuje, že horniny hledají nižší energetický stav (půdu), skalní struktura se nakonec rozpadne.

Tyto struktury jsou na mikroskopické úrovni (velikost živých buněk) namísto na nanoskopické (molekulární) úrovni, ale fungují jako pružiny, které uchovávají energii předanou šlehačem. Struktury se nerozpadnou okamžitě, protože tření jako síly protilehlých atrakcí vody se snaží držet vody při odpuzování oleje a ropa se snaží držet oleje při odpuzování vody.

Můžete si to představit jako lichoběžníkový oblouk s přitažlivostí voda-voda, která je odolná vůči tlaku a přitažlivost olej-olej je gravitace. (Kromě toho, že se to všechno děje ve třech rozměrech.) V oblouku je rovnováha gravitace a komprese stabilizována. Salátové zálivky jsou rovněž krátkodobě stabilní.

Molekulární pohyb nakonec způsobí, že se struktury pohnou z vyrovnání, jako je posunutí kamene v oblouku, a struktury se zhroutí a uvolní svou uloženou energii. Tato akumulovaná energie poté přesune vodu a olej zpět do jejich samostatných vrstev.

Takže systém jde odděleně (nízká energie) -> rozšlehaný (vysoká energie) -> odděleně (nízká energie).

Gravitace do procesu moc nepřidává, protože proces separace je poháněn energií přidanou šlehačem ve směsi. Gravitace jen způsobí hustší z obou ke dnu nádoby. Pokud jste udělali zálivku s nulovou gravitací, stále by se rozdělila na dvě kuličky, jen by se místo shora dolů orientovaly na sebe méně náhodně. (Zkoumali právě tento účinek, protože jeho chemický význam byl v 90. letech na raketoplánu a na mezinárodní vesmírné stanici.)

Zálivka na salát se neodděluje, protože používá emulgátor, obvykle lecitin, který působí jako lepidlo (nebo analogie malty v oblouku), což ztěžuje rozpad mikroskopických pružinových struktur. Vzhledem k dostatku času se však i ty oddělí.

Energie uložená v hydrofilně-hydrofobních kombinovaných systémech hraje v biochemii velkou roli, např. je to základní dynamika všech biologických membrán. Zpět na vysoké škole jsme vypočítali, kolik energie by se uvolnilo, kdybyste magicky způsobili, že se všechny vaše těla membrány zhroutí najednou. Nepamatuji si přesné číslo, ale pamatuji si, že to byl překvapivě velký boom.

Ropa se ve vodě konsoliduje, protože to zvyšuje entropii $ S $. Stoupá nahoru, protože to snižuje entalpii $ H $. Když se obě akce stanou společně, sníží to Gibbsovu volnou energii $ G $. $$ \ Delta G = \ Delta H - T \ Delta S $$

Jak poznamenal DavePhD, mezi páry molekul vody se tvoří vodíkové vazby. Jak komentoval Aaron Stevens v duplicitní otázce, „polární molekuly vody mají více konfigurací, aby vytvářely vodíkové vazby se svými sousedy.“ Zejména pokud jsou v nádobě molekuly vody ve výši $ N $, má daná molekula možné způsoby (termodynamické stavy) $ N $ k vytvoření jedné vodíkové vazby. (Technicky vzato, $ N-1 $, protože molekula se nemůže vázat na sebe, ale u velkého počtu molekul není rozdíl důležitý).

Pokud molekula vody vytvoří dvě vodíkové vazby, nyní existuje $ N ^ 2 $ způsob, jak to udělat. Se třemi vodíkovými vazbami, $ N ^ 3 $ způsoby. Vidíte, že s tím, jak se v nádobě tvoří více vodíkových vazeb, je možné více termodynamických stavů. To zvyšuje entropii.

Vodíkové vazby se netvoří mezi olejem a vodou ani mezi dvěma molekulami oleje. Když je molekula vody obklopena olejem, vytváří méně vodíkových vazeb a celková entropie klesá. Entropie je tedy maximalizována sloučením (shromážděním) oleje do souvislé hmoty, takže voda s ním naváže minimální kontakt.

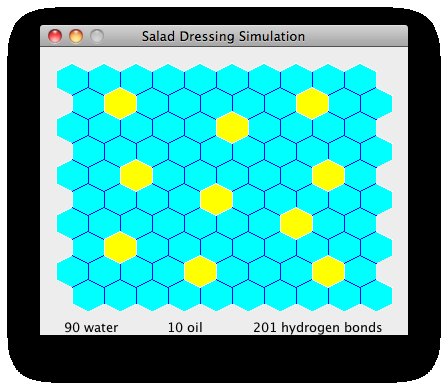
To ilustrují následující obrázky ze simulace, kterou jsem napsal k zodpovězení této otázky. Hexy jsou molekuly, 90 voda (azurová) a 10 olej (žlutá). Hranice mezi molekulami jsou nakresleny modře, pokud tvoří vodíkovou vazbu, a bílou, pokud ne. Celkový počet vodíkových vazeb je zobrazen ve spodní části simulace.

Prohlédněte si obrázek v horní části této odpovědi. Olej je dobře promíchán s vodou a voda tvoří 201 vodíkových vazeb.

Jak se olej začíná konsolidovat, molekuly vody mohou mezi sebou vytvářet více vodíkových vazeb (nyní 212):

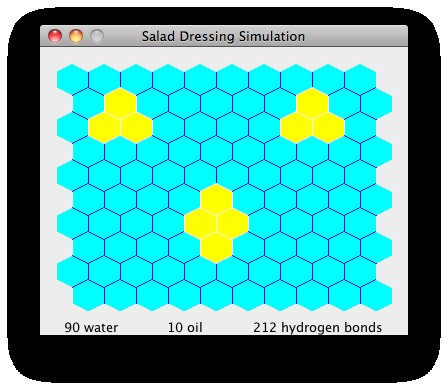
Když je olej plně konsolidovaný, může se vytvořit maximální počet vodíkových vazeb (233):

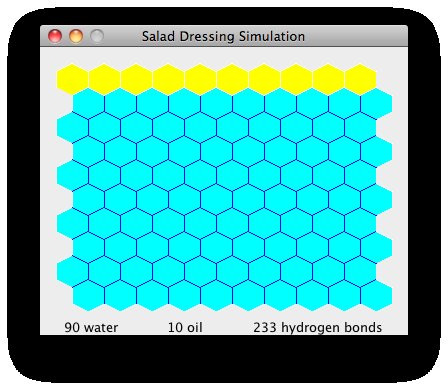
Vidíte, že počet vodíkových vazeb - a tím i entropie - je maximalizován při konsolidaci oleje.

Olej pluje (stoupá nahoru) kvůli entalpii. Konkrétně je potenciální energie směsi kombinovaná gravitační potenciální energie molekul. To je minimalizováno umístěním oleje nad vodu.

Při absenci gravitace se ropa bude konsolidovat, ale nebude plavat. Pokud je však přítomna gravitace, dojde k oběma efektům, aby se minimalizovala Gibbsova volná energie.

Dodatek: „Při absenci gravitace se ropa spojí, ale nebude plavat.“ Experimenty Mezinárodní vesmírné stanice to potvrzují:

Směsi koloidu a polymeru: Výsledky experimentů ISS studovaly spinodální rozklad nebo fázovou separaci poblíž kritického bodu, nezatížené rozdíly hustoty fází. Růst fázové separace byl studován pomocí rozptylu světla i zobrazování. Bez gravitace trvala fázová separace 30krát déle než na Zemi. Vzorek byl smíchán, poté byla zahájena fázová separace, která postupně zhrubla, dokud stěny nádoby neinteragovaly se směsí (po 42 hodinách) a fáze bohatá na koloidy navlhčila stěnu nádoby a po 60 hodinách ji zcela potáhla.

Kritický bod koloid-polymer: Okamžitě po smíchání se vzorek kritického bodu koloid-polymer začal rozdělovat do dvou fází - jedné, která připomínala plyn, a druhé, která připomínala kapalinu, kromě toho, že částice byly koloidy a ne atomy.Oblasti chudé na koloidy (koloidní? Plynná? Fáze) rostly větší, až nakonec bylo dosaženo úplného oddělení fází a do každé z nich byla jen jedna oblast - fáze bohatá na koloidy a fáze chudá na koloidy.Nic z tohoto chování nelze ve vzorku na Zemi pozorovat, protože sedimentace by způsobila, že koloidy padnou na dno buňky rychleji, než by mohlo dojít k procesu smíchání.Znalosti získané z těchto běhů byly použity k vývoji BCAT-3 později provozovaného na ISS.

EXPRESNÍ Fyzika koloidů ve vesmíru

Myslím si, že většina těchto vysvětlení není správná.

Stratifikace tekutin není řízena vazebnými interakcemi - tyto jednoduše řídí rychlost a ztrátu procesu. Stratifikace by v zásadě mohla být bezztrátová - neviditelná emulze by se stále stratifikovala, takže výše uvedené krásné vzorce z Wikipedie by se staly triviálními a neinstruktivními. Myslím, že odpověď je ve skutečnosti mnohem jednodušší.

Stratifikace je jen Archimédův princip. Domy jsou špinavé, protože existuje více způsobů, jak být špinavé než uklizené. Představte si dům posetý hračkami a pánvemi. Pokud přijde člověk a spojí všechny hračky do bodu v herně s elastickými lany a také se všemi pánvemi s kuchyní, nechá lana jít a všechny hračky letějí zhruba do herny a všechny pánve sklouznou podlahu do kuchyně. Dům je technicky upravenější, protože v jeho správné místnosti je méně způsobů uspořádání předmětů než v celém domě. Člověk, který navinul lana, musí samozřejmě degradovat své svalové cukry, aby to udělal, stejně jako proces, který smíchal uvedenou emulzi (myslím, že tlačí balón pod vodu). Stratifikace je jen uvolnění uložené potenciální energie, která vznikla v procesu míchání, který sám původně vyžadoval práci. Jakýkoli nepořádek lze uklidit uplatněním práce - právě to nakonec způsobí další nepořádek.