Tato odpověď není nic jiného než variace Sklivvovy odpovědi. Jednoduše bych chtěl probrat některé kvantitativní myšlenky vyplývající z odpovědi Sklivva a diskutovat o tom, co chápu (od přítele leteckého inženýrství) jako běžnou koncepční chybu - že použití „pouhého povrchového efektu“ a „aplikace Bernoulliho principu“ je špatné. Tyto „pouhé povrchové efekty a Bernoulliho princip“ vyplývají ze Sklivvova nápadu, jak doufám objasním. Všechno ve fyzice letadel začíná a končí „letadla tlačí vzduch dolů, takže vzduch tlačí letadla nahoru“ . Tato odpověď je napsána tak, aby byla srozumitelná pro někoho, jako jsem já, který neví nic o dynamice tekutin - kromě:
-
Matematicky elegantní a naprosto zábavné 2D problémy řešené složitou teorií proměnných (viz Nalezení stagnačních bodů z komplexního potenciálu);
-
Že vím, že pro každého, kdo může prokázat existenci, existuje cena Clay Mathematics nebo dát protiklad proti, existence hladkých, globálně dobře definovaných řešení Navier-Stokesových rovnic;
-
Že mi kolegové a přátelé z leteckého inženýrství říkají, že experimentální důkaz je v této oblasti stále královnou : nejreálnější dynamika tekutin zahrnující let letadla se silně opírá o fenomenologické modely vyladěné experimentem.
Odpovím tak, že tyto body postupně pozvednu.
Experiment je královna
Z konkrétního experimentálního hlediska , není záhadou, proč letouny létají. Lepší otázka podle mého názoru zní spíše: „jak ovládají nevyhnutelné obrovské síly, které na ně působí, aby se stabilně zvedly ve stálém vertikálním směru?“
Tento experimentální pohled je následující: pomyslete na Beaufortovu stupnici a další stupnice, které používají meteorologové k překročení praktického významu jejich větru a dalších varování: například Fujita Scale pro tornáda a Systémy kategorií tropických cyklónů, které v praxi popisují účinky bouří různé intenzity.
Nyní chápu, že předpisy o létání zakazují komerčním proudovým letounům létat pomaleji než 300 $ \ mathrm {km \, h ^ {- 1}} $ před konečným přiblížením na přistávací dráhu. Přemýšlejte o $ 300 \ mathrm {km \, h ^ {- 1}} $ rychlost letu, pokud jde o váhy, o kterých jsem právě mluvil: jedná se o tornádo F4, cyklón kategorie 5 a je daleko od Beaufortovy stupnice třídy 12. Budovy a konstrukce jakéhokoli tvaru, velikosti a hmotnosti plně naložených letadel jsou roztrhané a nesené do nebe nebo zcela strženy a zničeny. Neexistuje ŽÁDNÝ nedostatek výtahu z relativní rychlosti letu $ 300 \ mathrm {km \, h ^ {- 1}} $, která udrží téměř cokoli velikosti a hmotnosti plně naloženého komerčního tryskového letadla: při těchto rychlostech téměř cokoli této velikosti a hmotnosti a lehčích mušek. Přinejmenším to dělá prchavě: pokud není navrženo jako letadlo, protože se mění jeho postoje a mění se také směr tlaku beranu: je pravděpodobné, že bude převrácen a dopadne katastroficky na zem. Zjednodušeně řečeno: téměř všechno letí touto rychlostí, ale dělají to jen velmi zvláštní věci stabilně.
Jednoduché matematické modely
Můžeme udělat zadní část odhad obálky tlaku beranu v tomto případě: viz můj nákres níže jednoduchého křídla s výrazným úhlem náběhu drženého nehybně v aerodynamickém tunelu. Do popisu Sklivvze uvedu několik čísel:
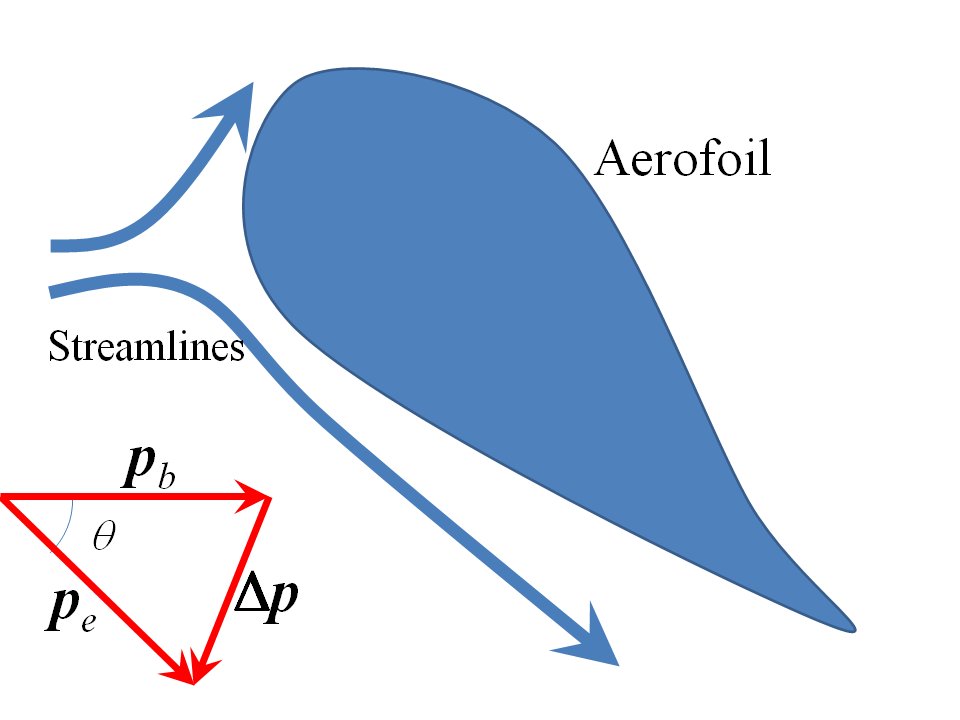
Předpokládejme, že proudění vzduchu je odkloněno o nějaký úhel $ \ theta $ radiány, aby bylo možné modelovat postoj (ne nadmořskou výšku) letounu při jeho posledním přiblížení k přistání nebo při jeho vzletu letícím 300 $ \ mathrm {km \, h ^ {-1}} $ rychlost letu nebo zhruba 80 $ \ mathrm {m \, s ^ {- 1}} $. Nakreslil jsem to strmým úhlem útoku. Vzduch blízko atmosférického tlaku na úrovni hladiny moře má hustotu přibližně 1,25 $ \ mathrm {kg \, m ^ {- 3}} $ (molární objem 0,0224 $ \ mathrm {m ^ {- 3}}) $. Je zobrazena změna diagramu hybnosti, odkud jsou změny složek vertikální a horizontální hybnosti (za předpokladu, že rychlost toku zůstane zhruba konstantní):
$$ \ Delta p_v = p_b \ sin \ theta; \ quad \ quad \ Delta p_h = p_b \, (1- \ cos \ theta) $$
Vychylovací křídlo současně představuje účinnou blokovací oblast pro kapalinu $ \ alpha \, A \ , \ sin \ theta $, kde $ A $ je skutečná plocha křídla a $ \ alpha $ měřítko, které zohledňuje skutečnost, že v ustáleném stavu je nejen kapalina těsně vedle křídla rozptýlena, takže efektivní plocha křídla bude být větší než jeho skutečná plocha. Hmotnost vzduchu vychýleného každou sekundu je tedy $ \ rho \, \ alfa \, A \, v \, \ sin \ theta $ a výtah $ L $ a tažení $ D $ (což si motory musí při vzletu dovolit) ) musí být:
$$ L = \ rho \, \ alpha \, A \, v ^ 2 \, (\ sin \ theta) ^ 2; \ quad \ quad D = \ rho \, \ alpha \, A \, v ^ 2 \, (1- \ cos \ theta) \, \ sin \ theta $$
Pokud připojíme úhel náběhu 30 stupňů, předpokládejme $ \ alpha = 1 $ a použijeme $ A = 1000 \ mathrm {m ^ 3} $ (zhruba to platí pro plochu křídla Airbusu A380), dostaneme zvedací síla $ L $ za $ \ rho = 1,25 \ mathrm {kg \, m ^ {- 3}} $ a $ v = 80 \ mathrm {m \, s ^ {- 1}} $ o hmotnosti 200 tun. To je poněkud méně než vzletová hmotnost plně naloženého Airbusu A380 (což je podle stránky Wikipedie A380) 592 tun, ale je to neuvěřitelně vysoká hmotnost stejná a ve správném pořadí velikost. Jak jsem řekl, experiment je tady královnou. Vidíme, že efektivní vertikální průřez křídla je větší než skutečné křídlo o faktor 2 až 3. To není překvapující v ustáleném stavu, hluboko pod rychlostí toku zvuku: tekutina se shlukuje a rušení je mnohem větší než jen kolem sousedství křídla. Když tedy zapojíme $ \ alpha = 3 $ (vzhledem k experimentální skutečnosti, že A380 se může zvednout s celkovou hmotností naloženého 592 tun), dostaneme odpor $ D $ o hmotnosti 54 tun (538 kN) - asi polovina plný tah 1,2 MN, takže to dobře souvisí se skutečnými specifikacemi Airbusu, protože v případě potřeby musí být k dispozici pohodlná rezerva, aby bylo možné letadlo z obtížnosti zvednout.
V těchto větrech stupně F4 / C5 (a až třikrát rychlejší za normálního letu), vidíme proto, že tam prostě není žádný nedostatek výtahu. Problém leteckého inženýrství spočívá spíše v udržení tohoto hojného vztlaku stabilně směřujícího nahoru a umožnění letounu udržovat stálý postoj a udržovat jakékoli točivé momenty vyplývající z nerovnoměrnosti výtahu z převrácení letadla.
Jak letadlo nabírá rychlost, výše vypočítaný tlak beranu je úměrný druhé mocnině rychlosti letu (viz moje odpověď na Tažnou sílu při vysokých rychlostech), takže při plné rychlosti účinek více než odpovídá poklesu hustoty vzduchu a mělčímu úhlu náběhu - nemůžeme tento tlak pístu dolů snížit, aniž bychom nepřekonali mnohem větší vodorovnou zadní část - táhnout se - takže pro dobrou účinnost paliva je důležité létat s malým úhlem náběhu.
Upřesnění matematického modelu
Je důležité dbát na to, že výše uvedený popis, pokud jde o rozdíl hybnosti mezi příchozím vzduchem a proplachem způsobeným dolním tokem křídlem, je přesně stejnou fyzikou jako „populárnější“ popis uvedený ve smyslu Bernoulliho rovnice a integrace tlaku kolem křídla. Je to dobře vidět: Navier-Stokesova rovnice ( Odvození Navier-Stokesovy rovnice naleznete na stránce Wikipedia), je velmi jednoduchá aplikace, která není ničím jiným než Newtonův druhý a třetí zákon pro nekonečně malé objemy tekutin, bez ohledu na nedostatek znalostí o jeho základních matematických vlastnostech (jak si to vyžádal status Clay Mathematics Millenium Prize: Miluji Navier-Stokesovu rovnici - tak jednoduchá, snadno uchopitelná myšlenka tak plešatě je jen ztělesněním Newtonových zákonů, přesto vyvolává hluboká tajemství, která nám vědcům ukazují, jak málo toho o světě zatím víme). Rovnice Navier Stokes v ustáleném stavu pro dokonalou nestlačitelnou tekutinu je (zde $ \ vec {v} $ je pole rychlosti ustáleného stavu a $ p $ pole skalárního tlaku):
$$ (\ vec {v} \ cdot \ nabla) \ vec {v} = \ nabla \ left (\ frac {| \ vec {v} | ^ 2} {2} \ right) + \ nabla \ wedge (\ nabla \ wedge \ vec {v}) = - \ nabla p $$
což dává $ \ nabla \ left (p + \ frac {| \ vec {v} | ^ 2} {2} \ right) = 0 $ nebo $ p + \ frac {| \ vec {v} | ^ 2} {2} = \ text {const} $ pro irrotační tok ($ \ nabla \ wedge \ vec {v} = \ vec {0} $) při integraci podél integrální křivky $ \ vec {v} $, tj. zefektivnit. Nebo můžeme v tomto jednoduchém případě argumentovat více prvními principy: síla na nekonečně malý objem je $ - \ nabla p $ a zrychlení částice na přímce je pomocí Serret-Frenetových vzorců (zde $ s $ je délka oblouku podél proudnice přes částici a $ \ kappa $ zakřivení cesty):
$$ \ mathrm {d} _t (v \ hat {\ mathbf {t} }) = \ mathrm {d} _s v \ times \ mathrm {d} _t s \, \ hat {\ mathbf {t}} + v \, \ mathrm {d} _s (\ hat {\ mathbf {t}} ) \, \ mathrm {d} _t s = v \, \ mathrm {d} _s v, \ hat {\ mathbf {t}} - \ kappa \, v ^ 2 \, \ hat {\ mathbf {n}} = \ mathrm {d} _s \ left (\ frac {v ^ 2} {2} \ right) \, \ hat {\ mathbf {t}} - \ kappa \, v ^ 2 \, \ hat {\ mathbf { n}} $$
odkud při aplikaci $ \ vec {F} = m \ vec {a} \ Rightarrow - \ nabla p \, \ mathrm {d} x \, \ mathrm {d} y \, \ mathrm {d} z = \ rho \, \ vec {a} \, \ mathrm {d} x \, \ mathrm {d} y \, \ mathrm {d} z $, dostaneme:
$$ - \ nabla p = \ rho \ left (\ mathrm {d} _s \ left (\ frac {v ^ 2} {2} \ right) \, \ hat {\ mathbf {t}} - \ kappa \, v ^ 2 \, \ hat {\ mathbf {n}} \ vpravo) $$
což opět dává $ p + \ frac {| \ vec {v} | ^ 2} {2} = const $ při integraci podél proudnice (zde vidíme bokem (normální proud) dostředivá síla $ -v ^ 2 \, \ hat {\ mathbf {n}} / R $ dané vítězným vzorcem $ v ^ 2 / R $). Můžeme tedy (a níže) například použít Blasiovu větu k výpočtu vztlaku a můžeme si být jisti, že to není nic jiného než kvantifikace Sklivvovy myšlenky, že „letadla tlačí vzduch dolů, takže vzduch tlačí letadla nahoru “. Tlakový rozdíl mezi horním a spodním povrchem křídla existuje protože křídlo tlačí vzduch dolů, nejedná se o samostatný jev. Často je slyšet, že Bernoulliho princip aplikovaný na křídla je špatný: to není pravda. Existuje omyl (o kterém bude pojednáno níže), jak je ukázáno experimentem (a teoreticky rukou) ve zvítězené demonstraci výtahu pomocí Bernoulliho principu, ale myšlenka je v zásadě zdravá, protože musí být odvozena od Navier-Stokesova rovnice a Newtonovy zákony uvedené výše.
Výpočet Joukowského aerofoilu a chyby v aplikaci Wontedova principu Bernoulliho na křídla
Podíváme se na 2D výpočet výtahu podle Bernoulliho principu nebo ekvivalentně použitím Blasiovy věty. Běžná mylná představa je, že proudění vzduchu se dělí na náběžné hraně křídla a dvě sousední částice se dostanou současně k zaostávající hraně křídla, takže horní částice musí při vyšších rychlostech ovlivňovat zakřivený povrch, a proto tlak na horní povrch křídla je méně. Ve skutečnosti jsou částice horní dráhy zrychleny mnohem víc, než toto vysvětlení naznačuje, a dosáhnou zaostávajícího okraje křídla daleko před svými sousedy, které se pohybují po nižší cestě. Podívejte se na toto nádherné video z University of Cambridge, zejména ve vzdálenosti asi 50 sekund. Tato skutečnost ukazuje, že oběh $ \ mast_ \ Gamma \ vec {v} \ cdot \ mathrm {d} \ vec { r} $ kolem povrchu křídla $ \ Gamma $ je nenulová, což je skutečnost, kterou intuitivně očekáváme od jednoduché teorie (jak je ukázáno níže) a která je dostatečně potvrzena v experimentu: podívejte se na video nebo jděte na konec dráhy velké letiště ve vlhkém dni, takže můžete nechat nad vámi létat velká komerční trysková letadla ve výšce asi 50 metrů (vezměte si chrániče sluchu). Ve vlhkém dni uvidíte víry, které odlamují vnější okraje křídel, uvidíte je vířit ve vlhkém vzduchu po několik sekund po probuzení letounu, a pokud si po průletu letadla sundáte ochranu sluchu, uslyšíte víry praskaly ve vzduchu a zněly trochu jako vlny omývané na pláži. To je mnohem zábavnější, než to zní, když vás vaše děti trápí, abyste něco takového udělali, a podle toho, jak to dělám, jsem se z toho naučil hromady více, než jsem si myslel. I když má následující výpočet nádech teoretické spolehlivosti a „prvních principů“, je důležité si uvědomit, že jde také o experimentální model : oběh je do našeho popisu vnucen, motivován potvrzení existence bývalého experimentem. Kutta-Joukowski podmínka (viz stránka Wikipedie pro Kutta podmínku) stejně jako stránka Wikipedie pro Kutta-Joukowski teorém je něco víc než experimentálně motivovaná oprava ad-hoc : je to prostě toto. Když modelujeme tok pomocí Joukowského křídla (popsáno níže), na křídle je ostrá zaostávající hrana. To plodí jedinečnost s nefyzickými, nekonečnými rychlostmi. Avšak postulováním a výběrem správné cirkulace v toku můžeme dát stagnační bod na zaostávající hranu, čímž zrušíme singularitu, usměrníme naše řešení a také vynutíme experimentálně pozorovanou podmínku, že u křídla je vždy jen jeden stagnační bod náběžná hrana, nikdy jinde.
Další způsob, jak nahlížet na tento experimentálně motivovaný stav, je dobře vysvětlen v této odpovědi na otázku Physics SE Má křídlo v potenciálním toku výtah?. Irotační, neviditelný, nestlačitelný tok nemůže sám zvednout křídlo. Přidáme oběh k „fudge“ jako kompenzaci za tento teoretický nedostatek: viskozita je „přírodní způsob vynucení Kutta-Joukowsského podmínky“.
Takže začneme metodou komplexní proměnné (viz Wikipedia stránka pro „Potenciální tok“ v sekci „Analýza pro dvourozměrný tok“ ke studiu potenciálního toku, tj. irrotačního ($ \ nabla \ wedge = \ vec {0} $) pole rychlosti $ \ vec {v} $ s potenciálním $ \ psi $ takovým, že $ \ vec {v} = - \ nabla \ psi $, který je také nestlačitelný (rovnice kontinuity $ \ nabla \ cdot \ vec {v} = \ nabla ^ 2 \ psi = 0 $ ). Viz také otázky fyziky SE Hledání stagnačních bodů z komplexního potenciálu).
Hlavní metodou je použití Joukowského transformace:
$ $ \ omega (z, \, s_z, \, s_ \ omega) = \ frac {s_ \ omega} {2} \ left (\ frac {z} {s_z} + \ frac {s_z} {z} \ vpravo) $$
Chcete-li mapovat potenciální tok odpovídající rotujícímu offsetovému válci ( viz stránka NASA „Zvednutí rotujícího válce“) do toku kolem obrazu tohoto válce pod Joukowského transformací. skutečně podivné Flettnerovo letadlo k úspěšnému letu skutečně použilo rotující válce, nikoli křídla. Joukowského transformace mapuje kruh $ | z | = s_z $ na skutečnou osu mezi body $ \ omega = \ pm s_ \ omega $ v rovině $ \ omega $; tato část skutečné osy mezi $ \ omega = \ pm s_ \ omega $ je pak odbočka pro inverzní Joukowského transformaci. Joukowského transformace je mapování dva ku jedné a větve inverzní Joukowského transformace mapují celou sféru $ \ omega $ -Riemann (pokud definujeme stereografickou projekci tak, že $ | z | = s_ \ omega $ je rovník $ \ omega $ -Riemann koule) odděleně dovnitř a mimo kruh $ | z | = s_z $ v rovině $ z $ (na které lze uvnitř i vně myslet severní a jižní polokouli sféry $ z $ -Riemann, pokud je zvolena stereografická projekce tak, že kruh $ | z | = s_z $ je rovník sféry $ z $ -Riemann). Povrch $ \ omega $ -Riemann je vytvořen rozřezáním dvou kopií Riemannovy koule podél řezu větve a sešitím okrajů dohromady, aby pro sféru $ \ omega $ -Riemann nevznikl dvojitý obal rodu. U tohoto problému definuji řez větve jako mírně odlišný od skutečného úseku osy mezi $ \ pm s_ \ omega $, definuji jej jako cestu:
$$ \ operatorname {Im} (\ omega) = h \ cos \ left (\ frac {\ pi} {2} \ operatorname {Re} (\ omega) \ right) $$
mezi dvěma body větvení s nastavitelným parametrem výšky $ h $, z důvodů, které budou jasné.
Poloměr $ r $ poloměru rotujícího válce je zvolen tak, aby povrch válce prošel bodem $ z = + s_z $, což je obrázek jednoho z bodů větve v rovině $ \ omega $. Tím je dosaženo ostré hrany, která se stává zaostávající hranou našeho křídla.
Komplexní potenciál rotujícího válce je:
$$ \ Omega (z) = v \, e ^ {- i \ alpha} \, \ left (z- \ delta \ right) + \ frac {r ^ 2 \, v \, e ^ {+ i \ alpha}} {z- \ delta} + i \, a \, \ log \ left (z - \ delta \ right) $$
kde $ \ alpha $ je úhel útoku, $ \ delta = \ delta_r + i \, \ delta_i $ je offset a $ r $ je poloměr válce strmý rovnoměrným tokem, který konverguje k $ v $ metrů za sekundu podél kladné reálné osy jako $ z \ to \ infty $. Logaritmus a dipólové výrazy dávají bod větve a pól do středu válce, takže tok je naprosto platný venku i na válci. $ a $ je oběh. Necháme-li $ \ phi $ znamenat úhlovou souřadnici označující okraj válce, jsou na válci dva stagnační body s úhlovými souřadnicemi $ \ phi_ \ pm $, kde $ \ mathrm {d} _z \ Omega (z ) = 0 $, ie když:
$$ e ^ {i \, (\ phi_ \ pm - \ alpha)} = -i \ frac {a} {2 \, v \, r} \ pm \ sqrt {1- \ left (\ frac {a} {2 \, v \, r} \ right) ^ 2} = \ exp \ left (- \ arcsin \ frac {a } {2 \, v \, r} \ right) $$
Nyní namapujeme tento tok do roviny $ \ omega $ a použijeme Blasiovu větu na obrázek ofsetové kružnice, aby se na tomto obrázku vyřešil výtah. Obrázek lze vykreslit pomocí příkazu Mathematica:
$$ \ small {\ mathrm {P [\ delta_r \ _, \ delta_i \ _]: = \\ ParametricPlot [\ {Re [\ omega [ \ delta_r + i \ delta_i + \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} Exp [i \ theta]], Im [\ omega [\ delta_r + i \ delta_i + \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} Exp [i \ theta]] \}, \ {\ theta, 0, 2 \ pi \}]}} $$
a výsledek se vykreslí níže v rovině $ \ omega $ za $ s_z = s_ \ omega = 1 $, $ \ delta_r = -0,1 $, $ \ delta_i = 0,3 $ ( tj. posun rotujícího kruhu tak, aby jeho centrum je na $ -0,1 + i \, 0,2 $ as poloměrem $ r = \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} $, takže jeho obraz prochází bodem větve $ \ omega = + s_ \ omega = 1 $ v letadle $ \ omega $:

Nyní se dostáváme k zásadnímu Kutta-Joukowského postulátu, experimentálnímu „fušerovi“. Ostrá hrana na nosném profilu nahoře by normálně mapovala tok v rovině $ z $, takže v tomto ostrém bodě byla nefyzická nekonečná rychlost. V praxi se při zkouškách v aerodynamickém tunelu ukazuje, že proudnice zůstávají tečny k hornímu povrchu a že na náběžné hraně křídla je jeden bod stagnace (intuitivně zde vzduch „naráží“) a žádné další silné > stagnační body na horní nebo dolní části křídla. Někdy existuje malá oblast turbulence kolem zaostávající hrany křídla (jako ve videu z University of Cambridge) (tj. Zde selže model nestlačitelného potenciálního toku) nebo se tok plynule odlepuje od zaostávající hrany. Způsob, jakým dosáhneme efektů podobných experimentu a „renormalizace“, je naše řešení přidat do průtoku správné množství oběhu $ a $ tak, aby jeden ze stagnačních bodů na rotujícím válci byl namapován na ostrou hranu (bod větvení na $ \ omega = + s_ \ omega $) v rovině $ \ omega $: stagnace tak ruší tam jinak nefyzické nekonečné rychlosti a „reguluje“ naše řešení. Když je poloměr válce zvolen jako $ r = \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} $, lze jej snadno zobrazit z výše uvedené rovnice pro polohy bodu stagnace, které potřebná cirkulace je:
$$ a = 2 v \, \ delta_i \ cos \ alpha + 2 \, v \, (1- \ delta_r) \ sin \ alpha $$
Toto je tedy plně experimentálně motivovaná Kutta-Joukowského podmínka. Je motivováno vědomím, že cirkulace je pozorována u křídel, experimentálně je na přední hraně kříže pouze jeden stagnační bod a skutečnost, že tyto experimentálně viděné výsledky může reprodukovat správné množství cirkulace.
Když je to hotové, výpočet vzestupu věty Blasius provedený kolem transformovaného Joukowského profilu v rovině $ \ omega $ je:
$$ \ begin {array} {lcl} D_ \ ell - i \, L_ \ ell & = & \ frac {i \, \ rho} {2} \ mast _ {\ Gamma_ \ omega} (\ mathrm { d} _ \ omega \ Omega) ^ 2 \, \ mathrm {d} \ omega \\ & = & \ frac {i \, \ rho} {2} \ mast _ {\ Gamma_z} (\ mathrm {d} _z \ Omega) ^ 2 \ frac {1} {\ mathrm {d} _z \ omega} \, \ mathrm {d} z \\ & = & - \ pi \, \ rho \ Sigma [\, \ mathrm {zbytky \, z \,} \, (\ mathrm {d} _z \ Omega) ^ 2 \ frac {1} {\ mathrm {d} _z \ omega} \, \ mathrm {v \, póly \, uvnitř \,} \ gama ] \\ & = & -4 \, \ pi \, i \, \ rho \, a \, v \, e ^ {- i \, \ alpha} \ end {pole} $$
kde $ \ Gamma_ \ omega $ je Joukowskiho profil a $ \ Gamma_z $ transformovaný profil ( tj. rotující válec). Neexistuje tedy žádný výtah bez oběhu. Stojí za to znovu uvést:
Irrotační, neviditelný a nestlačitelný tok nemůže sám zvednout křídlo. Přidáme oběh k „fudge“ kompenzaci za tento teoretický nedostatek: viskozita je „přírodní způsob vynucení Kutta-Joukowsského podmínky“.
Nyní nahradíme Kutta-Joukowského podmínku, abychom získali:
$$ D_ \ ell + i \, L_ \ ell = 8 \, \ pi \, i \, \ rho \, v ^ 2 \, \ left (\ delta_i \, \ cos \ alpha + (1- \ delta_r) \, \ sin \ alpha \ right) \ frac {s_z ^ 2} {s_ \ omega} e ^ {+ i \ alpha} $$
Nyní musíme škálovat rychlosti tak, aby relativní rychlosti letu byly v rovinách $ \ omega $ - a $ z $ rovny.
Výše uvedená je síla na jednotku délky (ve směru kolmém ke stránce) na křídle a jeho směr je směr v rovině $ \ omega $. Máme:
$$ \ lim \ limits _ {\ omega \ to \ infty} \ left (\ mathrm {d} _ \ omega \ Omega (\ omega (z)) \ right) = \ lim \ limits_ {z \ to \ infty} \ left (\ mathrm {d} _z \ Omega (\ omega (z)) \ right) \ lim \ limits _ {\ omega \ to \ infty} \ left (\ mathrm {d} _ \ omega z \ right) = 2 \, e ^ {- i \ alpha} v \ frac {s_z} {s_ \ omega} $$
takže potřebujeme $ s_ \ omega = 2 $ a $ s_z = 1 $, pak $ \ delta $ bude bezrozměrný parametr definující offset válce $ z $ -plane jako zlomek jeho poloměru. Nyní je ale šířka křídla planety $ \ omega $ 4 jednotky. Výše uvedený výpočet navíc poskytuje sílu na jednotku délky (kolmá k 2D toku). Výsledek pro $ s_ \ omega = 2 $ a $ s_z = 1 $ tedy vydělíme 4 a poté zvětšíme celkovou plochu křídla, abychom získali celkovou sílu na křídlo. Dále musíme otočit tok v náčrtu níže tak, aby příchozí tok byl vodorovný (tj. Ve směru relativní rychlosti vzduchu letounu) v celkové síle $ \ omega $ na křídle výše:
$$ D + i \, L = \ pi \, i \, \ rho \, v ^ 2 \, A \, \ left (\ delta_i \, \ cos \ alpha + (1- \ delta_r) \, \ sin \ alpha \ right) $$
Jsme svědky d'Alembertova paradoxu: dokonalý tok nemůže modelovat odpor. Nyní vložme několik čísel. Pokud dáme $ \ delta = 0 $, pak křídlo je prostě přímá větev rozříznutá mezi $ \ omega = \ pm 1 $, takže máme verzi výpočtu, kterou jsem začal, ale nyní je vylepšený zohlednit vzor plného toku. S $ \ alpha = 0,3 $ (o něco méně než 20 stupňů), $ \ rho = 1,25 \ mathrm {kg \, m ^ {- 3}} $, $ v = 80 \ mathrm {m \, s ^ {- 1}} $ a $ A = 850 \ mathrm {m ^ 2} $, dostaneme $ L = 643 \ mathrm {tonne} $, dost blízko plně naložené vzletové hmotnosti Airbusu. Pokud jsme zvolili parametry $ \ delta_i = 0,2 $, $ \ delta_r = -0,1 $, abychom získali tvar křídla, které se nezdá být příliš fantazijní pro křídlo tryskového dopravního letounu s klapkami zaostávajícími hranami, které jsou zcela vytaženy pro vzlet a přistání (viz graf níže) získáme asi 1200 tun výtah za naši rychlost $ 300 \ mathrm {km \, h ^ {- 1}} $. Je zřejmé, že je to optimistické a přepočet vychází z předpokladu stejné účinnosti celého rozpětí křídel, zatímco špičky nebudou 2D tokem zjevně dobře modelovány. Ne všechna křídla budou fungovat podle vzoru, takže $ A $ v tomto vzorci je o něco menší než plocha plánu. To, co ukazuje model proudění (viz níže), je však to, že efektivní vertikální průřez přiváděného vzduchu je mnohem větší, než nakloněná plocha $ A \, \ sin \ theta $ předpokládaná ve velmi jednoduchém modelu na začátku mé odpovědi. V ustáleném stavu je značný průřez vzduchu nad i pod svislým průřezem ohnut směrem dolů a přispívá k efektu „letadla tlačí vzduch dolů, takže vzduch tlačí letadla nahoru“ popsaného ve Sklivvově odpovědi.
K vykreslení celého transformovaného toku v rovině $ \ omega $ musíme použít inverzní Joukowského transformaci. Chcete-li to úspěšně provést, musíte použít správné větve inverzní transformace ve správných souřadnicových polích. Pro Mathematica, která umisťuje řez větve pro funkci odmocniny podél negativní skutečné osy (obor názvů std :: sqrt v Microsoft Visual C ++ ji umístí podél pozitivní skutečné osy ), definujeme následující funkce grafu, které jsou konkrétními větvemi inverzní transformace:
$$ \ zeta_1 (\ omega) = \ frac {s_z} {s_ \ omega} \ left (\ omega- i \ sqrt {\ omega-s_ \ omega} \, \ sqrt {- \ left (\ omega + s_ \ omega \ right)} \ right) $$$$ \ zeta_2 (\ omega) = \ frac {s_z} { s_ \ omega} \ left (\ omega + i \ sqrt {\ omega-s_ \ omega} \, \ sqrt {- \ left (\ omega + s_ \ omega \ right)} \ right) $$$$ \ zeta_3 (\ omega) = \ frac {s_z} {s_ \ omega} \ left (\ omega- \ sqrt {\ omega ^ 2-s_ \ omega ^ 2} \ right) $$$$ \ zeta_4 (\ omega) = \ frac { s_z} {s_ \ omega} \ left (\ omega + \ sqrt {\ omega ^ 2-s_ \ omega ^ 2} \ right) $$
a poté následující příkazy Mathematica vykreslí celý tok:
$$ \ small {\ mathrm {\ Omega [z \ _, \, \ delta \ _, \, v \ _, \, r \ _, \, a \ _, \, \ alpha \ _, \, s \ _]: = v \, e ^ {- i \, \ alpha} \ left (\ frac {z} {s} - \ delta \ right) + \ frac {r ^ 2 \ , v \, e ^ {i \, \ alpha}} {\ frac {z} {s} - \ delta} + i \, a \, Log \ left [\ frac {z} {s} - \ delta \ right]}} $$$$ \ small {\ mathrm {G [z \ _, \, \ delta_r \ _, \, \ delta_i \ _, \, \ alpha \ _]: = \ Omega \ left [z, \, \ delta_r + i \, \ delta_i, \, 1, \, \ sqrt {(1- \ delta_r) ^ 2 + \ delta_i ^ 2}, 2 \, \ delta_i Cos [\ alpha] + 2 \, (1- \ delta_r) \, Sin [\ alpha], \, \ alfa, \, 1 \ vpravo]}} $$
$$ \ small {\ mathrm {S [\ delta_r \ _, \ delta_i \ _, \ alpha \ _, h \ _, c \ _]: = \\ Zobrazit [ContourPlot [Im [If [(Abs [x] < 1) \ wedge (y > 0) \ wedge (y < h \, Cos [\ pi x / 2]), G [\ zeta_1 [x + iy], \ delta_r, \ delta_i, \ alpha]], Pokud [x < 0, G [\ zeta_3 [x + iy], \ delta_r, \ delta_i, \ alpha]], G [\ zeta_4 [x + iy], \ delta_r, \ delta_i, \ alpha ]]]]], \ {x, -2, 2 \}, \ {y, -2, 2 \}, obrysy \ do c, MaxRecursion \ do 2, PlotPoints \ do 300, AspectRatio \ do 1],
P [\ delta_r, \ delta_i, \ {Black, Thick \}]]}} $$
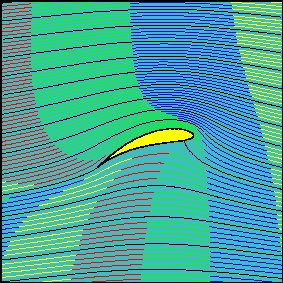
kde $ \ mathrm {P} [] $ je výše uvedený parametrický příkaz plotru, který se používá k vykreslení křídlového profilu. Výše uvedené použití funkcí větví funguje pro $ \ delta_r < 0 $: pro správné výsledky jsou potřeba další větve, když $ \ delta_r > 0 $. Parametr $ h $ ohýbá řez větve tak, aby se uklonil nahoru a zůstal uvnitř křídla, což umožňuje větvím inverzní Joukowského transformace správně vykreslit mapovaný tok válce. Níže je uveden výsledek z příkazu $ \ mathrm {S [-0,1, 0,2, 0,2, 0,2, 100]} $, tj. tok kolem křídla pro úhel útoku 0,2 radiánu, parametry offsetu kruhu $ -0,1 + 0,2 \, i $, úklona ve větvi je vyříznuta tak, že $ h = 0,2 $. Sledujte, jak se větev rozřízla uvnitř křídla dole, a také to, jak daleko od povrchu křídla se jeho účinek táhne. Efektivní vertikální složka plochy křídla, která je prezentována průtoku, je zjevně mnohem větší než skutečná vertikální složka plochy křídla, takže se zdá, že faktor 2 až 3 škálování ve výtahu Airbus A380, jak je počítán jednoduchým výpočtem průhybu kapaliny vysoce pravděpodobné a nepřekvapivé.

A konečně, aby se dostal do úplného kruhu, je zde na webových stránkách animace „Toky irrotační roviny neviditelné tekutiny“ na oddělení environmentálního inženýrství Univerzity v Janově; viz http://www.diam.unige.it/~irro/. Animace ukazuje průběh tekutých částic pro Joukowského tok křídla, ilustruje tvrzení, že tok nad křídlem prochází křídlem mnohem rychleji než proudění pod ním, a nakonec velmi dobře ukazuje hlavní tezi, že „letadla tlačí vzduch dolů“.